棋牌问答 大战红黑树
发布日期:2022-03-01 04:22 点击次数:159
概念红黑树是一种自平衡的二叉查找树,是一种高效的查找树.红黑树具有良好的效率, 它可在O(logN)时间内完成查找,增加,删除等操作.注意: 下文中, 非红色节点就是黑色节点, 即NULL节点是黑色节点特征节点是红色或黑色.根节点是黑色.每个叶子节点(NULL节点/空节点)是黑色.每个红色节点的两个孩子节点必须是黑色. (从叶子到根的所有路径上不能有两个连续的红色节点)从任意节点到其叶子节点的所有路径都包含相同数目的黑色节点.旋转当树的结构发生改变时(添加/删除元素时), 红黑树的五个特征可能会被打破, 需要通过调整结构和颜色使树重新满足红黑树的特征, 调整可以分为两类:颜色调整: 改变节点的颜色结构调整: 左旋 + 右旋左旋左旋就是成为右孩子的左孩子节点.左旋有以下三个步骤:将旋转节点的右节点的左节点关联到旋转节点的右节点上将旋转节点的父节点与旋转节点的右节点进行关联将旋转节点与旋转节点的右节点进行关联左旋示例图对节点30进行左旋的过程如下: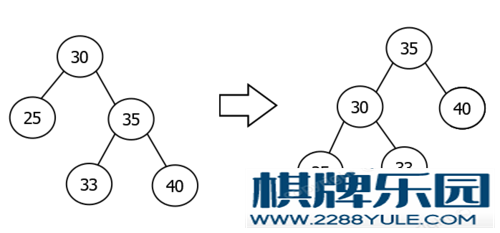 参考TreeMap的左旋代码/** From CLR */private void rotateLeft(Entry<K,V> p) {
// p为null就没意思了
if (p != null) {
// 获取p的右节点r, 临时存储
Entry<K,V> r = p.right;
// 步骤1
// 1. 将p的右节点的左节点连接到p的右节点上
p.right = r.left;
// 2. 将p的右节点的左节点的父节点指向为p
if (r.left != null)
r.left.parent = p;
// 步骤2
// 1. 将p的父节点赋值给r, r的父节点指向为p的父节点
r.parent = p.parent;
// 2-1. 父节点为空, 根节点即为r
if (p.parent == null)
root = r;
// 2-2. 父节点不为空, 判断p是父节点的左节点还是右节点, 然后进行关联
else if (p.parent.left == p) // p是父节点的左节点
p.parent.left = r;
else // p是父节点的右节点
p.parent.right = r;
// 步骤3
r.left = p;
p.parent = r;
}}
右旋右旋就是成为左孩子的右孩子节点.右旋有以下三个步骤(与左旋相反):将旋转节点的左节点的右节点关联到旋转节点的左节点上将旋转节点的父节点与旋转节点的左节点进行关联将旋转节点与旋转节点的左节点进行关联右旋示例图:对节点35进行右旋的过程如下:
参考TreeMap的左旋代码/** From CLR */private void rotateLeft(Entry<K,V> p) {
// p为null就没意思了
if (p != null) {
// 获取p的右节点r, 临时存储
Entry<K,V> r = p.right;
// 步骤1
// 1. 将p的右节点的左节点连接到p的右节点上
p.right = r.left;
// 2. 将p的右节点的左节点的父节点指向为p
if (r.left != null)
r.left.parent = p;
// 步骤2
// 1. 将p的父节点赋值给r, r的父节点指向为p的父节点
r.parent = p.parent;
// 2-1. 父节点为空, 根节点即为r
if (p.parent == null)
root = r;
// 2-2. 父节点不为空, 判断p是父节点的左节点还是右节点, 然后进行关联
else if (p.parent.left == p) // p是父节点的左节点
p.parent.left = r;
else // p是父节点的右节点
p.parent.right = r;
// 步骤3
r.left = p;
p.parent = r;
}}
右旋右旋就是成为左孩子的右孩子节点.右旋有以下三个步骤(与左旋相反):将旋转节点的左节点的右节点关联到旋转节点的左节点上将旋转节点的父节点与旋转节点的左节点进行关联将旋转节点与旋转节点的左节点进行关联右旋示例图:对节点35进行右旋的过程如下: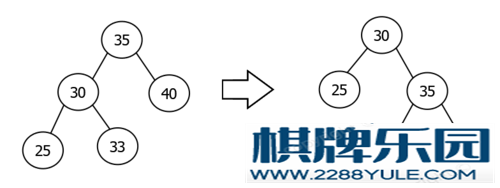 参考TreeMap的右旋代码:/** From CLR */private void rotateRight(Entry<K,V> p) {
// p为null就没意思了
if (p != null) {
// 临时存储p的左节点
Entry<K,V> l = p.left;
// 步骤1
p.left = l.right;
if (l.right != null)
l.right.parent = p;
// 步骤2
l.parent = p.parent;
if (p.parent == null)
root = l;
else if (p.parent.right == p)
p.parent.right = l;
else p.parent.left = l;
// 步骤3
l.right = p;
p.parent = l;
}}
寻找节点的后继当删除一个节点时, 需要找一个后继节点(也可以使用前驱, 这里我们使用后继)接替删除节点的位置, 那么如何寻找后继节点呢?参考TreeMap的寻找后继代码:/**
* Returns the successor of the specified Entry, or null if no such.
*/static <K,V> TreeMap.Entry<K,V> successor(Entry<K,V> t) {
if (t == null) // null is null
return null;
else if (t.right != null) { // 右节点非空
// 循环寻找右节点的左节点的左节点..., 直到左节点的左节点为空, 返回.
Entry<K,V> p = t.right;
while (p.left != null)
p = p.left;
return p;
} else { // 右节点非空
Entry<K,V> p = t.parent; // 父节点
Entry<K,V> ch = t; // 当前节点
while (p != null && ch == p.right) { // 当前节点是否是父节点的右节点
ch = p; // 获取父节点的引用
p = p.parent; // 父节点为祖父节点
}
// 如果当前节点不是父节点的右节点, 返回当前节点
return p;
}}
当然TreeMap中还有寻找节点的前驱的方法: Entry<K,V> predecessor(Entry<K,V> t).实际上前驱后继就是二叉树中序遍历时待删除节点的前驱后继.插入这里主要说红黑树是如何进行新元素插入之后的调节, 来重新让树成为一颗红黑树.插入的时候会出现以下四种情况:情况1: 新节点(当前节点)为根节点情况2: 新节点(当前节点)的父节点为黑色情况3: 新节点(当前节点)的父节点为红色 & 叔叔节点为红色情况4: 新节点(当前节点)的父节点为红色 & 叔叔节点为黑色下面分别说明各个情况时如何进行处理.情况1: 新节点(当前节点)为根节点直接将新节点(当前节点)染为黑色即可.示例图在一棵空树中插入节点20.
参考TreeMap的右旋代码:/** From CLR */private void rotateRight(Entry<K,V> p) {
// p为null就没意思了
if (p != null) {
// 临时存储p的左节点
Entry<K,V> l = p.left;
// 步骤1
p.left = l.right;
if (l.right != null)
l.right.parent = p;
// 步骤2
l.parent = p.parent;
if (p.parent == null)
root = l;
else if (p.parent.right == p)
p.parent.right = l;
else p.parent.left = l;
// 步骤3
l.right = p;
p.parent = l;
}}
寻找节点的后继当删除一个节点时, 需要找一个后继节点(也可以使用前驱, 这里我们使用后继)接替删除节点的位置, 那么如何寻找后继节点呢?参考TreeMap的寻找后继代码:/**
* Returns the successor of the specified Entry, or null if no such.
*/static <K,V> TreeMap.Entry<K,V> successor(Entry<K,V> t) {
if (t == null) // null is null
return null;
else if (t.right != null) { // 右节点非空
// 循环寻找右节点的左节点的左节点..., 直到左节点的左节点为空, 返回.
Entry<K,V> p = t.right;
while (p.left != null)
p = p.left;
return p;
} else { // 右节点非空
Entry<K,V> p = t.parent; // 父节点
Entry<K,V> ch = t; // 当前节点
while (p != null && ch == p.right) { // 当前节点是否是父节点的右节点
ch = p; // 获取父节点的引用
p = p.parent; // 父节点为祖父节点
}
// 如果当前节点不是父节点的右节点, 返回当前节点
return p;
}}
当然TreeMap中还有寻找节点的前驱的方法: Entry<K,V> predecessor(Entry<K,V> t).实际上前驱后继就是二叉树中序遍历时待删除节点的前驱后继.插入这里主要说红黑树是如何进行新元素插入之后的调节, 来重新让树成为一颗红黑树.插入的时候会出现以下四种情况:情况1: 新节点(当前节点)为根节点情况2: 新节点(当前节点)的父节点为黑色情况3: 新节点(当前节点)的父节点为红色 & 叔叔节点为红色情况4: 新节点(当前节点)的父节点为红色 & 叔叔节点为黑色下面分别说明各个情况时如何进行处理.情况1: 新节点(当前节点)为根节点直接将新节点(当前节点)染为黑色即可.示例图在一棵空树中插入节点20. 情况2: 新节点(当前节点)的父节点为黑色父节点是黑色, 添加一个红色孩子节点并不会影响红黑树的性质, 不需要调整.示例图在一棵红黑树中插入节点33, 因为父节点是黑色, 所以不需要进行调整即可.
情况2: 新节点(当前节点)的父节点为黑色父节点是黑色, 添加一个红色孩子节点并不会影响红黑树的性质, 不需要调整.示例图在一棵红黑树中插入节点33, 因为父节点是黑色, 所以不需要进行调整即可.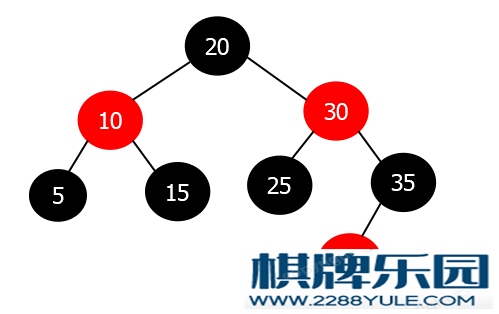 情况3: 新节点(当前节点)的父节点为红色 & 叔叔节点为红色祖父节点一定为黑色.处理步骤:将父节点和叔叔节点染为黑色将祖父节点染为红色将新节点(当前节点)指向为祖父节点该情况与当前节点是父节点的左孩子还是右孩子无关, 因为不涉及旋转.这时新节点(当前节点)的颜色还是红色, 可能出现四种情况:情况1: 新节点(当前节点)为根节点情况2: 新节点(当前节点)的父节点为黑色情况3: 新节点(当前节点)的叔叔节点为红色情况4: 新节点(当前节点)的叔叔节点为黑色然后再进入对应情况的处理方案中处理.示例图在红黑树中插入节点8(X), 插入之后的红黑树如下:
情况3: 新节点(当前节点)的父节点为红色 & 叔叔节点为红色祖父节点一定为黑色.处理步骤:将父节点和叔叔节点染为黑色将祖父节点染为红色将新节点(当前节点)指向为祖父节点该情况与当前节点是父节点的左孩子还是右孩子无关, 因为不涉及旋转.这时新节点(当前节点)的颜色还是红色, 可能出现四种情况:情况1: 新节点(当前节点)为根节点情况2: 新节点(当前节点)的父节点为黑色情况3: 新节点(当前节点)的叔叔节点为红色情况4: 新节点(当前节点)的叔叔节点为黑色然后再进入对应情况的处理方案中处理.示例图在红黑树中插入节点8(X), 插入之后的红黑树如下: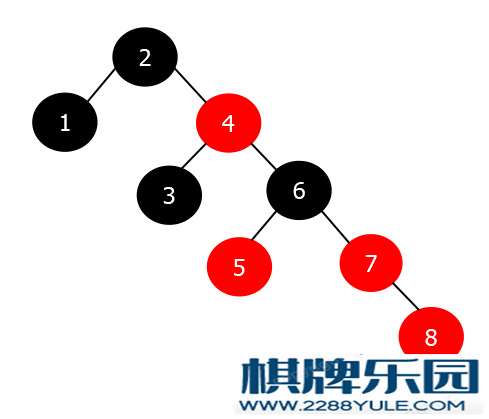 很明显违反了红黑树的性质5, 需要进行调整, 按照情况3的处理步骤进行调整, 调整之后的红黑树如下:
很明显违反了红黑树的性质5, 需要进行调整, 按照情况3的处理步骤进行调整, 调整之后的红黑树如下: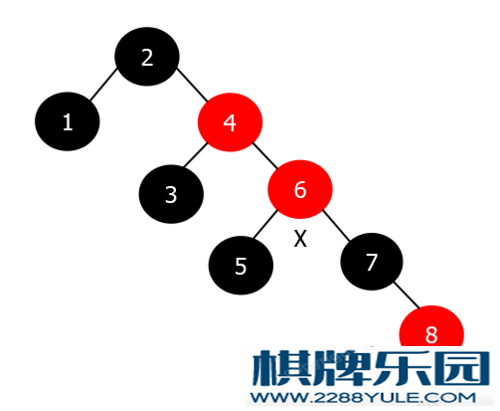 然后将当前节点(X)指向祖父节点, 继续进行其它情况的调整.情况4: 新节点(当前节点)的父节点为红色 & 叔叔节点为黑色处理步骤(父节点是祖父节点的左节点):判断新节点(当前节点)是否是父节点的右孩子节点(将当前节点调整为父节点的左孩子节点)是: 新节点(当前节点)指向父节点, 然后对当前节点进行左旋否: 不作处理将父节点染为黑色将祖父节点染为红色对祖父节点进行右旋处理步骤(父节点是祖父节点的右节点):判断新节点(当前节点)是否是父节点的左孩子节点(将当前节点调整为父节点的右孩子节点)是: 新节点(当前节点)指向父节点, 然后对当前节点进行右旋否: 不作处理将父节点染为黑色将祖父节点染为红色对祖父节点进行左旋以当前节点是父节点的左节点为例, 步骤1-1完成之后, 就变为当前节点是父节点的左孩子节点, 并且叔叔节点是黑色. 如果当前节点本就是父节点的左孩子节点, 则不进行处理, 直接进入步骤2.这时新节点的的颜色还是红色, 兄弟节点的颜色为红色, 父节点为黑色, 可能出现四种情况:情况1: 新节点(当前节点)为根节点情况2: 新节点(当前节点)的父节点为黑色情况3: 新节点(当前节点)的叔叔节点为红色情况4: 新节点(当前节点)的叔叔节点为黑色然后再进入对应情况的处理方案中处理.示例图继续调整情况3中的红黑树:
然后将当前节点(X)指向祖父节点, 继续进行其它情况的调整.情况4: 新节点(当前节点)的父节点为红色 & 叔叔节点为黑色处理步骤(父节点是祖父节点的左节点):判断新节点(当前节点)是否是父节点的右孩子节点(将当前节点调整为父节点的左孩子节点)是: 新节点(当前节点)指向父节点, 然后对当前节点进行左旋否: 不作处理将父节点染为黑色将祖父节点染为红色对祖父节点进行右旋处理步骤(父节点是祖父节点的右节点):判断新节点(当前节点)是否是父节点的左孩子节点(将当前节点调整为父节点的右孩子节点)是: 新节点(当前节点)指向父节点, 然后对当前节点进行右旋否: 不作处理将父节点染为黑色将祖父节点染为红色对祖父节点进行左旋以当前节点是父节点的左节点为例, 步骤1-1完成之后, 就变为当前节点是父节点的左孩子节点, 并且叔叔节点是黑色. 如果当前节点本就是父节点的左孩子节点, 则不进行处理, 直接进入步骤2.这时新节点的的颜色还是红色, 兄弟节点的颜色为红色, 父节点为黑色, 可能出现四种情况:情况1: 新节点(当前节点)为根节点情况2: 新节点(当前节点)的父节点为黑色情况3: 新节点(当前节点)的叔叔节点为红色情况4: 新节点(当前节点)的叔叔节点为黑色然后再进入对应情况的处理方案中处理.示例图继续调整情况3中的红黑树: 按照情况4进行调整之后, 调整之后的红黑树如下:
按照情况4进行调整之后, 调整之后的红黑树如下: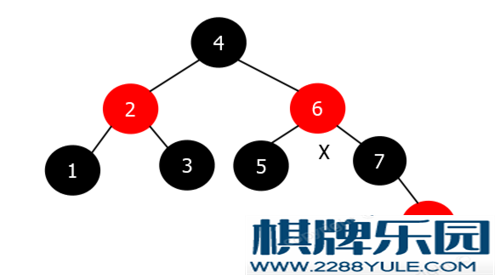 调整完成.插入总结当新插入一个元素时, 先按照二叉排序树的方法进行元素的插入, 之后将新元素的颜色染为红色, 然后对树进行调整, 使其重新成为红黑树.参考TreeMap的插入调整代码/** From CLR */private void fixAfterInsertion(Entry<K,V> x) {
// 默认新节点的颜色为红色
x.color = RED;
// 父节点为黑色时, 增加一个红色节点并不会影响红黑树
while (x != null && x != root && x.parent.color == RED) {
// 父节点为祖父节点的左节点
if (parentOf(x) == leftOf(parentOf(parentOf(x)))) {
// 获取叔叔节点
Entry<K,V> y = rightOf(parentOf(parentOf(x)));
if (colorOf(y) == RED) { // 叔叔节点为红色时
// 父节点和兄弟节点染为黑色
setColor(parentOf(x), BLACK);
setColor(y, BLACK);
// 祖父节点染为红色
setColor(parentOf(parentOf(x)), RED);
// 当前节点指向为祖父节点
x = parentOf(parentOf(x));
} else { // 叔叔节点为黑色时
// 判断当前节点的左右
// 将当前节点调整为父节点的左节点
if (x == rightOf(parentOf(x))) {
x = parentOf(x);
rotateLeft(x);
}
// 父节点染为黑色
setColor(parentOf(x), BLACK);
// 祖父节点染为红色
setColor(parentOf(parentOf(x)), RED);
// 对祖父节点进行右旋
rotateRight(parentOf(parentOf(x)));
}
} else {
Entry<K,V> y = leftOf(parentOf(parentOf(x)));
if (colorOf(y) == RED) {
setColor(parentOf(x), BLACK);
setColor(y, BLACK);
setColor(parentOf(parentOf(x)), RED);
x = parentOf(parentOf(x));
} else {
if (x == leftOf(parentOf(x))) {
x = parentOf(x);
rotateRight(x);
}
setColor(parentOf(x), BLACK);
setColor(parentOf(parentOf(x)), RED);
rotateLeft(parentOf(parentOf(x)));
}
}
}
// 最后将根节点染为黑色? 为什么需要这段代码, 我觉得你应该知道的.
root.color = BLACK;}
删除相对于插入, 红黑树的删除操作要复杂的多, 不过我们拆解分析, 就简单了, 把复杂问题拆解为小问题.对于一颗红黑树, 其删除节点的情况可以分为3种:情况1: 节点既有左子树又有右子树情况2: 节点只有左子树或只有右子树情况3: 节点既没有左子树又没有右子树(叶子节点)对于情况1, 我们首先要找到该节点的前驱或后继节点, 使用前驱或后继节点的值覆盖待删除节点的值, 然后将前驱或后继节点按照情况2或情况3进行删除即可. 前驱或者后继节点顶多有一个子节点.所以, 对于红黑树来说, 实际删除节点的情况只有两种(情况2和情况3).情况2出现的情况情况2-1: 待删除节点为红色情况2-1-1: 待删除节点的右孩子为黑色(不存在)情况2-1-2: 待删除节点的右孩子为红色(不存在)情况2-1-3: 待删除节点的左孩子为黑色(不存在)情况2-1-4: 待删除节点的左孩子为红色(不存在)情况2-2: 待删除节点为黑色情况2-2-1: 待删除节点的右孩子为黑色(不存在)情况2-2-2: 待删除节点的右孩子为红色情况2-2-3: 待删除节点的左子树为黑色(不存在)情况2-2-4: 待删除节点的左孩子为红色分析情况2, 只有情况2-2-2和情况2-2-4成立, 而这两种情况下只需要把红色节点删除即可.其它情况并不符合红黑树的特性, 所以根本不会存在其它情况的删除.情况2-2-2: 待删除节点为黑色 & 待删除节点的右孩子为红色处理步骤:将其右孩子链接到其父节点上.将右孩子染为黑色即可.这种情况就是普通的节点删除操作示例图在下图红黑树中, 要删除节点25
调整完成.插入总结当新插入一个元素时, 先按照二叉排序树的方法进行元素的插入, 之后将新元素的颜色染为红色, 然后对树进行调整, 使其重新成为红黑树.参考TreeMap的插入调整代码/** From CLR */private void fixAfterInsertion(Entry<K,V> x) {
// 默认新节点的颜色为红色
x.color = RED;
// 父节点为黑色时, 增加一个红色节点并不会影响红黑树
while (x != null && x != root && x.parent.color == RED) {
// 父节点为祖父节点的左节点
if (parentOf(x) == leftOf(parentOf(parentOf(x)))) {
// 获取叔叔节点
Entry<K,V> y = rightOf(parentOf(parentOf(x)));
if (colorOf(y) == RED) { // 叔叔节点为红色时
// 父节点和兄弟节点染为黑色
setColor(parentOf(x), BLACK);
setColor(y, BLACK);
// 祖父节点染为红色
setColor(parentOf(parentOf(x)), RED);
// 当前节点指向为祖父节点
x = parentOf(parentOf(x));
} else { // 叔叔节点为黑色时
// 判断当前节点的左右
// 将当前节点调整为父节点的左节点
if (x == rightOf(parentOf(x))) {
x = parentOf(x);
rotateLeft(x);
}
// 父节点染为黑色
setColor(parentOf(x), BLACK);
// 祖父节点染为红色
setColor(parentOf(parentOf(x)), RED);
// 对祖父节点进行右旋
rotateRight(parentOf(parentOf(x)));
}
} else {
Entry<K,V> y = leftOf(parentOf(parentOf(x)));
if (colorOf(y) == RED) {
setColor(parentOf(x), BLACK);
setColor(y, BLACK);
setColor(parentOf(parentOf(x)), RED);
x = parentOf(parentOf(x));
} else {
if (x == leftOf(parentOf(x))) {
x = parentOf(x);
rotateRight(x);
}
setColor(parentOf(x), BLACK);
setColor(parentOf(parentOf(x)), RED);
rotateLeft(parentOf(parentOf(x)));
}
}
}
// 最后将根节点染为黑色? 为什么需要这段代码, 我觉得你应该知道的.
root.color = BLACK;}
删除相对于插入, 红黑树的删除操作要复杂的多, 不过我们拆解分析, 就简单了, 把复杂问题拆解为小问题.对于一颗红黑树, 其删除节点的情况可以分为3种:情况1: 节点既有左子树又有右子树情况2: 节点只有左子树或只有右子树情况3: 节点既没有左子树又没有右子树(叶子节点)对于情况1, 我们首先要找到该节点的前驱或后继节点, 使用前驱或后继节点的值覆盖待删除节点的值, 然后将前驱或后继节点按照情况2或情况3进行删除即可. 前驱或者后继节点顶多有一个子节点.所以, 对于红黑树来说, 实际删除节点的情况只有两种(情况2和情况3).情况2出现的情况情况2-1: 待删除节点为红色情况2-1-1: 待删除节点的右孩子为黑色(不存在)情况2-1-2: 待删除节点的右孩子为红色(不存在)情况2-1-3: 待删除节点的左孩子为黑色(不存在)情况2-1-4: 待删除节点的左孩子为红色(不存在)情况2-2: 待删除节点为黑色情况2-2-1: 待删除节点的右孩子为黑色(不存在)情况2-2-2: 待删除节点的右孩子为红色情况2-2-3: 待删除节点的左子树为黑色(不存在)情况2-2-4: 待删除节点的左孩子为红色分析情况2, 只有情况2-2-2和情况2-2-4成立, 而这两种情况下只需要把红色节点删除即可.其它情况并不符合红黑树的特性, 所以根本不会存在其它情况的删除.情况2-2-2: 待删除节点为黑色 & 待删除节点的右孩子为红色处理步骤:将其右孩子链接到其父节点上.将右孩子染为黑色即可.这种情况就是普通的节点删除操作示例图在下图红黑树中, 要删除节点25 按照上述的处理步骤进行调整, 调整之后的红黑树如下:
按照上述的处理步骤进行调整, 调整之后的红黑树如下: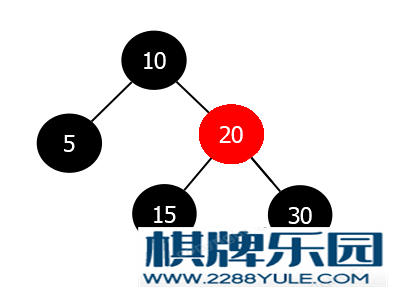 直接把孩子节点染为黑色, 然后替换被删除节点的位置即可.情况2-2-2: 待删除节点为黑色 & 待删除节点的左孩子为红色处理步骤:将其左孩子链接到其父节点上.将左孩子染为黑色即可.这种情况就是普通的节点删除操作.示例图如同情况2-2-1的示例图, 只不过孩子节点在左边而已.情况3出现的情况情况3-1: 待删除节点为黑色情况3-1-1: 兄弟节点为红色情况3-1-2: 兄弟节点为黑色 & 兄弟节点的两个孩子有一个为红色情况3-1-3: 兄弟节点为黑色 & 兄弟节点的两个孩子都是黑色(包括NULL节点)情况3-2: 待删除节点为红色情况3-1-1: 待删除节点为黑色 & 兄弟节点为红色处理步骤(待删除节点是父节点的左孩子):父节点染为红色兄弟节点染为黑色对父节点进行左旋重新计算兄弟节点处理步骤(待删除节点是父节点的右孩子):父节点染为红色兄弟节点染为黑色对父节点进行右旋重新计算兄弟节点这时, 父节点为红色, 兄弟节点为黑色, 进入其它情况.示例图在下图红黑树中, 要删除节点5
直接把孩子节点染为黑色, 然后替换被删除节点的位置即可.情况2-2-2: 待删除节点为黑色 & 待删除节点的左孩子为红色处理步骤:将其左孩子链接到其父节点上.将左孩子染为黑色即可.这种情况就是普通的节点删除操作.示例图如同情况2-2-1的示例图, 只不过孩子节点在左边而已.情况3出现的情况情况3-1: 待删除节点为黑色情况3-1-1: 兄弟节点为红色情况3-1-2: 兄弟节点为黑色 & 兄弟节点的两个孩子有一个为红色情况3-1-3: 兄弟节点为黑色 & 兄弟节点的两个孩子都是黑色(包括NULL节点)情况3-2: 待删除节点为红色情况3-1-1: 待删除节点为黑色 & 兄弟节点为红色处理步骤(待删除节点是父节点的左孩子):父节点染为红色兄弟节点染为黑色对父节点进行左旋重新计算兄弟节点处理步骤(待删除节点是父节点的右孩子):父节点染为红色兄弟节点染为黑色对父节点进行右旋重新计算兄弟节点这时, 父节点为红色, 兄弟节点为黑色, 进入其它情况.示例图在下图红黑树中, 要删除节点5 按照上述的处理步骤进行调整, 调整之后的红黑树如下:
按照上述的处理步骤进行调整, 调整之后的红黑树如下: 这时还是不符合红黑树的性质, 需要进一步调整, 这时进入情况3-1-3.情况3-1-2: 待删除节点为黑色 & 兄弟节点为黑色 & 兄弟节点的两个孩子有一个为红色处理步骤(待删除节点是父节点的左孩子):判断兄弟节点的右节点是否是黑色(NULL节点为黑色)将兄弟节点的左孩子染为黑色将兄弟节点染为红色对兄弟节点进行右旋重新计算兄弟节点将兄弟节点的颜色染为父节点的颜色将父节点染为黑色将兄弟节点的右孩子染为黑色对父节点进行左旋处理步骤(待删除节点是父节点的右孩子):判断兄弟节点的左节点是否是黑色(NULL节点为黑色)将兄弟节点的右孩子染为黑色将兄弟节点染为红色对兄弟节点进行左旋重新计算兄弟节点将兄弟节点的颜色染为父节点的颜色将父节点染为黑色将兄弟节点的右孩子染为黑色对父节点进行右旋示例图以待删除节点是父节点的左孩子为例, 在下图红黑树中, 要删除节点15
这时还是不符合红黑树的性质, 需要进一步调整, 这时进入情况3-1-3.情况3-1-2: 待删除节点为黑色 & 兄弟节点为黑色 & 兄弟节点的两个孩子有一个为红色处理步骤(待删除节点是父节点的左孩子):判断兄弟节点的右节点是否是黑色(NULL节点为黑色)将兄弟节点的左孩子染为黑色将兄弟节点染为红色对兄弟节点进行右旋重新计算兄弟节点将兄弟节点的颜色染为父节点的颜色将父节点染为黑色将兄弟节点的右孩子染为黑色对父节点进行左旋处理步骤(待删除节点是父节点的右孩子):判断兄弟节点的左节点是否是黑色(NULL节点为黑色)将兄弟节点的右孩子染为黑色将兄弟节点染为红色对兄弟节点进行左旋重新计算兄弟节点将兄弟节点的颜色染为父节点的颜色将父节点染为黑色将兄弟节点的右孩子染为黑色对父节点进行右旋示例图以待删除节点是父节点的左孩子为例, 在下图红黑树中, 要删除节点15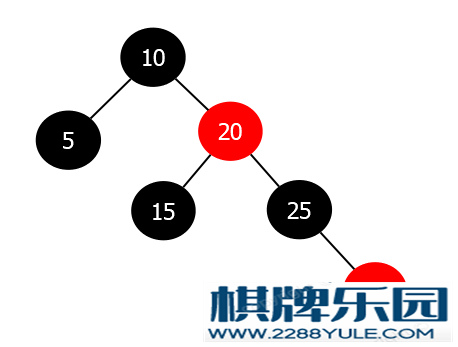 按照上述的处理步骤进行调整, 调整之后的红黑树如下:
按照上述的处理步骤进行调整, 调整之后的红黑树如下: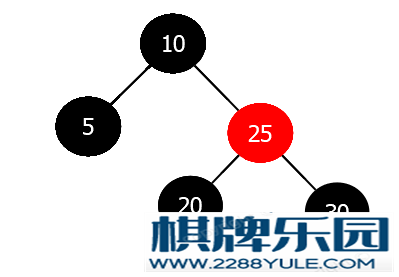 调整完成.中间我们省略了步骤1中的处理步骤, 内部的处理步骤同插入时的调整类似, 把兄弟节点的红色孩子节点调整兄弟节点的右孩子(如果兄弟节点是左孩子的话, 那么就是将红色孩子节点调整为左孩子).其实这种情况下, 我们不关系待删除节点的父节点的颜色, 因为这种情况的调整是在内部进行调整的.情况3-1-3: 待删除节点为黑色 & 兄弟节点为黑色 & 兄弟节点的两个孩子都是黑色(包括NULL节点)注: 这里兄弟的孩子节点包括NULL节点.处理步骤:将兄弟节点染为红色将父节点染为黑色该情况与当待删除节点是父节点的左孩子还是右孩子无关, 因为不涉及旋转.当前节点指向父节点之后, 再看符合哪种调整情况, 继续进行调整.示例图情况3-1-1中调整之后树为:
调整完成.中间我们省略了步骤1中的处理步骤, 内部的处理步骤同插入时的调整类似, 把兄弟节点的红色孩子节点调整兄弟节点的右孩子(如果兄弟节点是左孩子的话, 那么就是将红色孩子节点调整为左孩子).其实这种情况下, 我们不关系待删除节点的父节点的颜色, 因为这种情况的调整是在内部进行调整的.情况3-1-3: 待删除节点为黑色 & 兄弟节点为黑色 & 兄弟节点的两个孩子都是黑色(包括NULL节点)注: 这里兄弟的孩子节点包括NULL节点.处理步骤:将兄弟节点染为红色将父节点染为黑色该情况与当待删除节点是父节点的左孩子还是右孩子无关, 因为不涉及旋转.当前节点指向父节点之后, 再看符合哪种调整情况, 继续进行调整.示例图情况3-1-1中调整之后树为: 按照上述的处理步骤进行调整, 调整之后的红黑树如下:
按照上述的处理步骤进行调整, 调整之后的红黑树如下: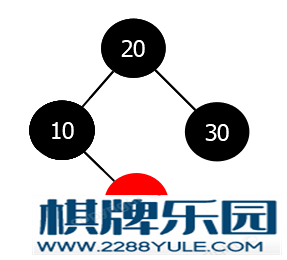 调整完成.情况3-2: 待删除节点为红色这时, 父节点为黑色, 兄弟节点一定为红色. 因为此时待删除节点和兄弟节点都没有孩子节点.直接删除就好.删除总结删除时, 先看待删除节点的颜色, 然后查看其兄弟节点的颜色, 再查看兄弟节点的孩子节点的颜色, 然后根据具体的情况进行调整.参考TreeMap的删除调整代码/** From CLR */private void fixAfterDeletion(Entry<K,V> x) {
// 删除的节点为黑色时, 需要进行调整
while (x != root && colorOf(x) == BLACK) {
// 当前节点是左节点
if (x == leftOf(parentOf(x))) {
// 获取右节点(兄弟节点)
Entry<K,V> sib = rightOf(parentOf(x));
// 兄弟节点是红色时
if (colorOf(sib) == RED) {
// 兄弟节点染为黑色
setColor(sib, BLACK);
// 父节点染为红色
setColor(parentOf(x), RED);
// 对父节点进行左旋
rotateLeft(parentOf(x));
// 重新计算兄弟节点
sib = rightOf(parentOf(x));
}
if (colorOf(leftOf(sib)) == BLACK &&
colorOf(rightOf(sib)) == BLACK) { // 兄弟节点的两个孩子都是黑色
// 兄弟节点染为红色
setColor(sib, RED);
// 将当前节点指向父节点
x = parentOf(x);
} else { // 兄弟节点的两个孩子有一个为红色
// 判断兄弟节点红色孩子节点的位置
// 将兄弟节点的红色孩子节点调整到兄弟节点的右孩子节点位置
if (colorOf(rightOf(sib)) == BLACK) {
setColor(leftOf(sib), BLACK);
setColor(sib, RED);
rotateRight(sib);
sib = rightOf(parentOf(x));
}
// 将兄弟节点的颜色染为父节点的颜色
setColor(sib, colorOf(parentOf(x)));
// 父节点染为黑色
setColor(parentOf(x), BLACK);
// 兄弟节点的右孩子染为黑色
setColor(rightOf(sib), BLACK);
// 对父节点进行左旋
rotateLeft(parentOf(x));
// 退出循环
x = root;
}
} else { // symmetric
Entry<K,V> sib = leftOf(parentOf(x));
if (colorOf(sib) == RED) {
setColor(sib, BLACK);
setColor(parentOf(x), RED);
rotateRight(parentOf(x));
sib = leftOf(parentOf(x));
}
if (colorOf(rightOf(sib)) == BLACK &&
colorOf(leftOf(sib)) == BLACK) {
setColor(sib, RED);
x = parentOf(x);
} else {
if (colorOf(leftOf(sib)) == BLACK) {
setColor(rightOf(sib), BLACK);
setColor(sib, RED);
rotateLeft(sib);
sib = leftOf(parentOf(x));
}
setColor(sib, colorOf(parentOf(x)));
setColor(parentOf(x), BLACK);
setColor(leftOf(sib), BLACK);
rotateRight(parentOf(x));
x = root;
}
}
}
// 最后将当前节点染为黑色, 为什么需要这段代码? 我觉得你应该知道的.
setColor(x, BLACK);}
总结红黑树是一个比较重要的算法, 我觉得作为一个程序员应该需要了解它.红黑树的核心在于元素变动之后, 如何进行调整使其重新成为一颗红黑树.通过学习红黑树, 深刻体会到大问题并不可怕, 一点点拆分为小问题, 一定会解决的.文章不是一气呵成的, 个别地方可能会有问题, 如有发现, 烦请指出.JAVA算法作者:黑色毛衣Virgo链接:http://www.imooc.com/article/247142来源:慕课网本文原创发布于慕课网 ,转载请注明出处,谢谢合作推荐阅读:藏在正则表达式里的陷阱对于新手来说,Python 中有哪些难以理解的概念?Git使用教程,最详细,最傻瓜,最浅显,真正手把手教为什么部分程序员下班后只关显示器不关电脑?推荐10个Java方向最热门的开源项目为什么程序员应该有一台Mac个人电脑有哪些好笑的关于程序员的笑话?如何防止自己被人肉搜索到?如何写代码 —— 编程内功心法搞定JVM垃圾回收就是这么简单搞定计算机网络面试,看这篇就够了(补充版)
调整完成.情况3-2: 待删除节点为红色这时, 父节点为黑色, 兄弟节点一定为红色. 因为此时待删除节点和兄弟节点都没有孩子节点.直接删除就好.删除总结删除时, 先看待删除节点的颜色, 然后查看其兄弟节点的颜色, 再查看兄弟节点的孩子节点的颜色, 然后根据具体的情况进行调整.参考TreeMap的删除调整代码/** From CLR */private void fixAfterDeletion(Entry<K,V> x) {
// 删除的节点为黑色时, 需要进行调整
while (x != root && colorOf(x) == BLACK) {
// 当前节点是左节点
if (x == leftOf(parentOf(x))) {
// 获取右节点(兄弟节点)
Entry<K,V> sib = rightOf(parentOf(x));
// 兄弟节点是红色时
if (colorOf(sib) == RED) {
// 兄弟节点染为黑色
setColor(sib, BLACK);
// 父节点染为红色
setColor(parentOf(x), RED);
// 对父节点进行左旋
rotateLeft(parentOf(x));
// 重新计算兄弟节点
sib = rightOf(parentOf(x));
}
if (colorOf(leftOf(sib)) == BLACK &&
colorOf(rightOf(sib)) == BLACK) { // 兄弟节点的两个孩子都是黑色
// 兄弟节点染为红色
setColor(sib, RED);
// 将当前节点指向父节点
x = parentOf(x);
} else { // 兄弟节点的两个孩子有一个为红色
// 判断兄弟节点红色孩子节点的位置
// 将兄弟节点的红色孩子节点调整到兄弟节点的右孩子节点位置
if (colorOf(rightOf(sib)) == BLACK) {
setColor(leftOf(sib), BLACK);
setColor(sib, RED);
rotateRight(sib);
sib = rightOf(parentOf(x));
}
// 将兄弟节点的颜色染为父节点的颜色
setColor(sib, colorOf(parentOf(x)));
// 父节点染为黑色
setColor(parentOf(x), BLACK);
// 兄弟节点的右孩子染为黑色
setColor(rightOf(sib), BLACK);
// 对父节点进行左旋
rotateLeft(parentOf(x));
// 退出循环
x = root;
}
} else { // symmetric
Entry<K,V> sib = leftOf(parentOf(x));
if (colorOf(sib) == RED) {
setColor(sib, BLACK);
setColor(parentOf(x), RED);
rotateRight(parentOf(x));
sib = leftOf(parentOf(x));
}
if (colorOf(rightOf(sib)) == BLACK &&
colorOf(leftOf(sib)) == BLACK) {
setColor(sib, RED);
x = parentOf(x);
} else {
if (colorOf(leftOf(sib)) == BLACK) {
setColor(rightOf(sib), BLACK);
setColor(sib, RED);
rotateLeft(sib);
sib = leftOf(parentOf(x));
}
setColor(sib, colorOf(parentOf(x)));
setColor(parentOf(x), BLACK);
setColor(leftOf(sib), BLACK);
rotateRight(parentOf(x));
x = root;
}
}
}
// 最后将当前节点染为黑色, 为什么需要这段代码? 我觉得你应该知道的.
setColor(x, BLACK);}
总结红黑树是一个比较重要的算法, 我觉得作为一个程序员应该需要了解它.红黑树的核心在于元素变动之后, 如何进行调整使其重新成为一颗红黑树.通过学习红黑树, 深刻体会到大问题并不可怕, 一点点拆分为小问题, 一定会解决的.文章不是一气呵成的, 个别地方可能会有问题, 如有发现, 烦请指出.JAVA算法作者:黑色毛衣Virgo链接:http://www.imooc.com/article/247142来源:慕课网本文原创发布于慕课网 ,转载请注明出处,谢谢合作推荐阅读:藏在正则表达式里的陷阱对于新手来说,Python 中有哪些难以理解的概念?Git使用教程,最详细,最傻瓜,最浅显,真正手把手教为什么部分程序员下班后只关显示器不关电脑?推荐10个Java方向最热门的开源项目为什么程序员应该有一台Mac个人电脑有哪些好笑的关于程序员的笑话?如何防止自己被人肉搜索到?如何写代码 —— 编程内功心法搞定JVM垃圾回收就是这么简单搞定计算机网络面试,看这篇就够了(补充版)
 参考TreeMap的左旋代码/** From CLR */private void rotateLeft(Entry<K,V> p) {
// p为null就没意思了
if (p != null) {
// 获取p的右节点r, 临时存储
Entry<K,V> r = p.right;
// 步骤1
// 1. 将p的右节点的左节点连接到p的右节点上
p.right = r.left;
// 2. 将p的右节点的左节点的父节点指向为p
if (r.left != null)
r.left.parent = p;
// 步骤2
// 1. 将p的父节点赋值给r, r的父节点指向为p的父节点
r.parent = p.parent;
// 2-1. 父节点为空, 根节点即为r
if (p.parent == null)
root = r;
// 2-2. 父节点不为空, 判断p是父节点的左节点还是右节点, 然后进行关联
else if (p.parent.left == p) // p是父节点的左节点
p.parent.left = r;
else // p是父节点的右节点
p.parent.right = r;
// 步骤3
r.left = p;
p.parent = r;
}}
右旋右旋就是成为左孩子的右孩子节点.右旋有以下三个步骤(与左旋相反):将旋转节点的左节点的右节点关联到旋转节点的左节点上将旋转节点的父节点与旋转节点的左节点进行关联将旋转节点与旋转节点的左节点进行关联右旋示例图:对节点35进行右旋的过程如下:
参考TreeMap的左旋代码/** From CLR */private void rotateLeft(Entry<K,V> p) {
// p为null就没意思了
if (p != null) {
// 获取p的右节点r, 临时存储
Entry<K,V> r = p.right;
// 步骤1
// 1. 将p的右节点的左节点连接到p的右节点上
p.right = r.left;
// 2. 将p的右节点的左节点的父节点指向为p
if (r.left != null)
r.left.parent = p;
// 步骤2
// 1. 将p的父节点赋值给r, r的父节点指向为p的父节点
r.parent = p.parent;
// 2-1. 父节点为空, 根节点即为r
if (p.parent == null)
root = r;
// 2-2. 父节点不为空, 判断p是父节点的左节点还是右节点, 然后进行关联
else if (p.parent.left == p) // p是父节点的左节点
p.parent.left = r;
else // p是父节点的右节点
p.parent.right = r;
// 步骤3
r.left = p;
p.parent = r;
}}
右旋右旋就是成为左孩子的右孩子节点.右旋有以下三个步骤(与左旋相反):将旋转节点的左节点的右节点关联到旋转节点的左节点上将旋转节点的父节点与旋转节点的左节点进行关联将旋转节点与旋转节点的左节点进行关联右旋示例图:对节点35进行右旋的过程如下: 参考TreeMap的右旋代码:/** From CLR */private void rotateRight(Entry<K,V> p) {
// p为null就没意思了
if (p != null) {
// 临时存储p的左节点
Entry<K,V> l = p.left;
// 步骤1
p.left = l.right;
if (l.right != null)
l.right.parent = p;
// 步骤2
l.parent = p.parent;
if (p.parent == null)
root = l;
else if (p.parent.right == p)
p.parent.right = l;
else p.parent.left = l;
// 步骤3
l.right = p;
p.parent = l;
}}
寻找节点的后继当删除一个节点时, 需要找一个后继节点(也可以使用前驱, 这里我们使用后继)接替删除节点的位置, 那么如何寻找后继节点呢?参考TreeMap的寻找后继代码:/**
* Returns the successor of the specified Entry, or null if no such.
*/static <K,V> TreeMap.Entry<K,V> successor(Entry<K,V> t) {
if (t == null) // null is null
return null;
else if (t.right != null) { // 右节点非空
// 循环寻找右节点的左节点的左节点..., 直到左节点的左节点为空, 返回.
Entry<K,V> p = t.right;
while (p.left != null)
p = p.left;
return p;
} else { // 右节点非空
Entry<K,V> p = t.parent; // 父节点
Entry<K,V> ch = t; // 当前节点
while (p != null && ch == p.right) { // 当前节点是否是父节点的右节点
ch = p; // 获取父节点的引用
p = p.parent; // 父节点为祖父节点
}
// 如果当前节点不是父节点的右节点, 返回当前节点
return p;
}}
当然TreeMap中还有寻找节点的前驱的方法: Entry<K,V> predecessor(Entry<K,V> t).实际上前驱后继就是二叉树中序遍历时待删除节点的前驱后继.插入这里主要说红黑树是如何进行新元素插入之后的调节, 来重新让树成为一颗红黑树.插入的时候会出现以下四种情况:情况1: 新节点(当前节点)为根节点情况2: 新节点(当前节点)的父节点为黑色情况3: 新节点(当前节点)的父节点为红色 & 叔叔节点为红色情况4: 新节点(当前节点)的父节点为红色 & 叔叔节点为黑色下面分别说明各个情况时如何进行处理.情况1: 新节点(当前节点)为根节点直接将新节点(当前节点)染为黑色即可.示例图在一棵空树中插入节点20.
参考TreeMap的右旋代码:/** From CLR */private void rotateRight(Entry<K,V> p) {
// p为null就没意思了
if (p != null) {
// 临时存储p的左节点
Entry<K,V> l = p.left;
// 步骤1
p.left = l.right;
if (l.right != null)
l.right.parent = p;
// 步骤2
l.parent = p.parent;
if (p.parent == null)
root = l;
else if (p.parent.right == p)
p.parent.right = l;
else p.parent.left = l;
// 步骤3
l.right = p;
p.parent = l;
}}
寻找节点的后继当删除一个节点时, 需要找一个后继节点(也可以使用前驱, 这里我们使用后继)接替删除节点的位置, 那么如何寻找后继节点呢?参考TreeMap的寻找后继代码:/**
* Returns the successor of the specified Entry, or null if no such.
*/static <K,V> TreeMap.Entry<K,V> successor(Entry<K,V> t) {
if (t == null) // null is null
return null;
else if (t.right != null) { // 右节点非空
// 循环寻找右节点的左节点的左节点..., 直到左节点的左节点为空, 返回.
Entry<K,V> p = t.right;
while (p.left != null)
p = p.left;
return p;
} else { // 右节点非空
Entry<K,V> p = t.parent; // 父节点
Entry<K,V> ch = t; // 当前节点
while (p != null && ch == p.right) { // 当前节点是否是父节点的右节点
ch = p; // 获取父节点的引用
p = p.parent; // 父节点为祖父节点
}
// 如果当前节点不是父节点的右节点, 返回当前节点
return p;
}}
当然TreeMap中还有寻找节点的前驱的方法: Entry<K,V> predecessor(Entry<K,V> t).实际上前驱后继就是二叉树中序遍历时待删除节点的前驱后继.插入这里主要说红黑树是如何进行新元素插入之后的调节, 来重新让树成为一颗红黑树.插入的时候会出现以下四种情况:情况1: 新节点(当前节点)为根节点情况2: 新节点(当前节点)的父节点为黑色情况3: 新节点(当前节点)的父节点为红色 & 叔叔节点为红色情况4: 新节点(当前节点)的父节点为红色 & 叔叔节点为黑色下面分别说明各个情况时如何进行处理.情况1: 新节点(当前节点)为根节点直接将新节点(当前节点)染为黑色即可.示例图在一棵空树中插入节点20. 情况2: 新节点(当前节点)的父节点为黑色父节点是黑色, 添加一个红色孩子节点并不会影响红黑树的性质, 不需要调整.示例图在一棵红黑树中插入节点33, 因为父节点是黑色, 所以不需要进行调整即可.
情况2: 新节点(当前节点)的父节点为黑色父节点是黑色, 添加一个红色孩子节点并不会影响红黑树的性质, 不需要调整.示例图在一棵红黑树中插入节点33, 因为父节点是黑色, 所以不需要进行调整即可. 情况3: 新节点(当前节点)的父节点为红色 & 叔叔节点为红色祖父节点一定为黑色.处理步骤:将父节点和叔叔节点染为黑色将祖父节点染为红色将新节点(当前节点)指向为祖父节点该情况与当前节点是父节点的左孩子还是右孩子无关, 因为不涉及旋转.这时新节点(当前节点)的颜色还是红色, 可能出现四种情况:情况1: 新节点(当前节点)为根节点情况2: 新节点(当前节点)的父节点为黑色情况3: 新节点(当前节点)的叔叔节点为红色情况4: 新节点(当前节点)的叔叔节点为黑色然后再进入对应情况的处理方案中处理.示例图在红黑树中插入节点8(X), 插入之后的红黑树如下:
情况3: 新节点(当前节点)的父节点为红色 & 叔叔节点为红色祖父节点一定为黑色.处理步骤:将父节点和叔叔节点染为黑色将祖父节点染为红色将新节点(当前节点)指向为祖父节点该情况与当前节点是父节点的左孩子还是右孩子无关, 因为不涉及旋转.这时新节点(当前节点)的颜色还是红色, 可能出现四种情况:情况1: 新节点(当前节点)为根节点情况2: 新节点(当前节点)的父节点为黑色情况3: 新节点(当前节点)的叔叔节点为红色情况4: 新节点(当前节点)的叔叔节点为黑色然后再进入对应情况的处理方案中处理.示例图在红黑树中插入节点8(X), 插入之后的红黑树如下: 很明显违反了红黑树的性质5, 需要进行调整, 按照情况3的处理步骤进行调整, 调整之后的红黑树如下:
很明显违反了红黑树的性质5, 需要进行调整, 按照情况3的处理步骤进行调整, 调整之后的红黑树如下: 然后将当前节点(X)指向祖父节点, 继续进行其它情况的调整.情况4: 新节点(当前节点)的父节点为红色 & 叔叔节点为黑色处理步骤(父节点是祖父节点的左节点):判断新节点(当前节点)是否是父节点的右孩子节点(将当前节点调整为父节点的左孩子节点)是: 新节点(当前节点)指向父节点, 然后对当前节点进行左旋否: 不作处理将父节点染为黑色将祖父节点染为红色对祖父节点进行右旋处理步骤(父节点是祖父节点的右节点):判断新节点(当前节点)是否是父节点的左孩子节点(将当前节点调整为父节点的右孩子节点)是: 新节点(当前节点)指向父节点, 然后对当前节点进行右旋否: 不作处理将父节点染为黑色将祖父节点染为红色对祖父节点进行左旋以当前节点是父节点的左节点为例, 步骤1-1完成之后, 就变为当前节点是父节点的左孩子节点, 并且叔叔节点是黑色. 如果当前节点本就是父节点的左孩子节点, 则不进行处理, 直接进入步骤2.这时新节点的的颜色还是红色, 兄弟节点的颜色为红色, 父节点为黑色, 可能出现四种情况:情况1: 新节点(当前节点)为根节点情况2: 新节点(当前节点)的父节点为黑色情况3: 新节点(当前节点)的叔叔节点为红色情况4: 新节点(当前节点)的叔叔节点为黑色然后再进入对应情况的处理方案中处理.示例图继续调整情况3中的红黑树:
然后将当前节点(X)指向祖父节点, 继续进行其它情况的调整.情况4: 新节点(当前节点)的父节点为红色 & 叔叔节点为黑色处理步骤(父节点是祖父节点的左节点):判断新节点(当前节点)是否是父节点的右孩子节点(将当前节点调整为父节点的左孩子节点)是: 新节点(当前节点)指向父节点, 然后对当前节点进行左旋否: 不作处理将父节点染为黑色将祖父节点染为红色对祖父节点进行右旋处理步骤(父节点是祖父节点的右节点):判断新节点(当前节点)是否是父节点的左孩子节点(将当前节点调整为父节点的右孩子节点)是: 新节点(当前节点)指向父节点, 然后对当前节点进行右旋否: 不作处理将父节点染为黑色将祖父节点染为红色对祖父节点进行左旋以当前节点是父节点的左节点为例, 步骤1-1完成之后, 就变为当前节点是父节点的左孩子节点, 并且叔叔节点是黑色. 如果当前节点本就是父节点的左孩子节点, 则不进行处理, 直接进入步骤2.这时新节点的的颜色还是红色, 兄弟节点的颜色为红色, 父节点为黑色, 可能出现四种情况:情况1: 新节点(当前节点)为根节点情况2: 新节点(当前节点)的父节点为黑色情况3: 新节点(当前节点)的叔叔节点为红色情况4: 新节点(当前节点)的叔叔节点为黑色然后再进入对应情况的处理方案中处理.示例图继续调整情况3中的红黑树: 按照情况4进行调整之后, 调整之后的红黑树如下:
按照情况4进行调整之后, 调整之后的红黑树如下: 调整完成.插入总结当新插入一个元素时, 先按照二叉排序树的方法进行元素的插入, 之后将新元素的颜色染为红色, 然后对树进行调整, 使其重新成为红黑树.参考TreeMap的插入调整代码/** From CLR */private void fixAfterInsertion(Entry<K,V> x) {
// 默认新节点的颜色为红色
x.color = RED;
// 父节点为黑色时, 增加一个红色节点并不会影响红黑树
while (x != null && x != root && x.parent.color == RED) {
// 父节点为祖父节点的左节点
if (parentOf(x) == leftOf(parentOf(parentOf(x)))) {
// 获取叔叔节点
Entry<K,V> y = rightOf(parentOf(parentOf(x)));
if (colorOf(y) == RED) { // 叔叔节点为红色时
// 父节点和兄弟节点染为黑色
setColor(parentOf(x), BLACK);
setColor(y, BLACK);
// 祖父节点染为红色
setColor(parentOf(parentOf(x)), RED);
// 当前节点指向为祖父节点
x = parentOf(parentOf(x));
} else { // 叔叔节点为黑色时
// 判断当前节点的左右
// 将当前节点调整为父节点的左节点
if (x == rightOf(parentOf(x))) {
x = parentOf(x);
rotateLeft(x);
}
// 父节点染为黑色
setColor(parentOf(x), BLACK);
// 祖父节点染为红色
setColor(parentOf(parentOf(x)), RED);
// 对祖父节点进行右旋
rotateRight(parentOf(parentOf(x)));
}
} else {
Entry<K,V> y = leftOf(parentOf(parentOf(x)));
if (colorOf(y) == RED) {
setColor(parentOf(x), BLACK);
setColor(y, BLACK);
setColor(parentOf(parentOf(x)), RED);
x = parentOf(parentOf(x));
} else {
if (x == leftOf(parentOf(x))) {
x = parentOf(x);
rotateRight(x);
}
setColor(parentOf(x), BLACK);
setColor(parentOf(parentOf(x)), RED);
rotateLeft(parentOf(parentOf(x)));
}
}
}
// 最后将根节点染为黑色? 为什么需要这段代码, 我觉得你应该知道的.
root.color = BLACK;}
删除相对于插入, 红黑树的删除操作要复杂的多, 不过我们拆解分析, 就简单了, 把复杂问题拆解为小问题.对于一颗红黑树, 其删除节点的情况可以分为3种:情况1: 节点既有左子树又有右子树情况2: 节点只有左子树或只有右子树情况3: 节点既没有左子树又没有右子树(叶子节点)对于情况1, 我们首先要找到该节点的前驱或后继节点, 使用前驱或后继节点的值覆盖待删除节点的值, 然后将前驱或后继节点按照情况2或情况3进行删除即可. 前驱或者后继节点顶多有一个子节点.所以, 对于红黑树来说, 实际删除节点的情况只有两种(情况2和情况3).情况2出现的情况情况2-1: 待删除节点为红色情况2-1-1: 待删除节点的右孩子为黑色(不存在)情况2-1-2: 待删除节点的右孩子为红色(不存在)情况2-1-3: 待删除节点的左孩子为黑色(不存在)情况2-1-4: 待删除节点的左孩子为红色(不存在)情况2-2: 待删除节点为黑色情况2-2-1: 待删除节点的右孩子为黑色(不存在)情况2-2-2: 待删除节点的右孩子为红色情况2-2-3: 待删除节点的左子树为黑色(不存在)情况2-2-4: 待删除节点的左孩子为红色分析情况2, 只有情况2-2-2和情况2-2-4成立, 而这两种情况下只需要把红色节点删除即可.其它情况并不符合红黑树的特性, 所以根本不会存在其它情况的删除.情况2-2-2: 待删除节点为黑色 & 待删除节点的右孩子为红色处理步骤:将其右孩子链接到其父节点上.将右孩子染为黑色即可.这种情况就是普通的节点删除操作示例图在下图红黑树中, 要删除节点25
调整完成.插入总结当新插入一个元素时, 先按照二叉排序树的方法进行元素的插入, 之后将新元素的颜色染为红色, 然后对树进行调整, 使其重新成为红黑树.参考TreeMap的插入调整代码/** From CLR */private void fixAfterInsertion(Entry<K,V> x) {
// 默认新节点的颜色为红色
x.color = RED;
// 父节点为黑色时, 增加一个红色节点并不会影响红黑树
while (x != null && x != root && x.parent.color == RED) {
// 父节点为祖父节点的左节点
if (parentOf(x) == leftOf(parentOf(parentOf(x)))) {
// 获取叔叔节点
Entry<K,V> y = rightOf(parentOf(parentOf(x)));
if (colorOf(y) == RED) { // 叔叔节点为红色时
// 父节点和兄弟节点染为黑色
setColor(parentOf(x), BLACK);
setColor(y, BLACK);
// 祖父节点染为红色
setColor(parentOf(parentOf(x)), RED);
// 当前节点指向为祖父节点
x = parentOf(parentOf(x));
} else { // 叔叔节点为黑色时
// 判断当前节点的左右
// 将当前节点调整为父节点的左节点
if (x == rightOf(parentOf(x))) {
x = parentOf(x);
rotateLeft(x);
}
// 父节点染为黑色
setColor(parentOf(x), BLACK);
// 祖父节点染为红色
setColor(parentOf(parentOf(x)), RED);
// 对祖父节点进行右旋
rotateRight(parentOf(parentOf(x)));
}
} else {
Entry<K,V> y = leftOf(parentOf(parentOf(x)));
if (colorOf(y) == RED) {
setColor(parentOf(x), BLACK);
setColor(y, BLACK);
setColor(parentOf(parentOf(x)), RED);
x = parentOf(parentOf(x));
} else {
if (x == leftOf(parentOf(x))) {
x = parentOf(x);
rotateRight(x);
}
setColor(parentOf(x), BLACK);
setColor(parentOf(parentOf(x)), RED);
rotateLeft(parentOf(parentOf(x)));
}
}
}
// 最后将根节点染为黑色? 为什么需要这段代码, 我觉得你应该知道的.
root.color = BLACK;}
删除相对于插入, 红黑树的删除操作要复杂的多, 不过我们拆解分析, 就简单了, 把复杂问题拆解为小问题.对于一颗红黑树, 其删除节点的情况可以分为3种:情况1: 节点既有左子树又有右子树情况2: 节点只有左子树或只有右子树情况3: 节点既没有左子树又没有右子树(叶子节点)对于情况1, 我们首先要找到该节点的前驱或后继节点, 使用前驱或后继节点的值覆盖待删除节点的值, 然后将前驱或后继节点按照情况2或情况3进行删除即可. 前驱或者后继节点顶多有一个子节点.所以, 对于红黑树来说, 实际删除节点的情况只有两种(情况2和情况3).情况2出现的情况情况2-1: 待删除节点为红色情况2-1-1: 待删除节点的右孩子为黑色(不存在)情况2-1-2: 待删除节点的右孩子为红色(不存在)情况2-1-3: 待删除节点的左孩子为黑色(不存在)情况2-1-4: 待删除节点的左孩子为红色(不存在)情况2-2: 待删除节点为黑色情况2-2-1: 待删除节点的右孩子为黑色(不存在)情况2-2-2: 待删除节点的右孩子为红色情况2-2-3: 待删除节点的左子树为黑色(不存在)情况2-2-4: 待删除节点的左孩子为红色分析情况2, 只有情况2-2-2和情况2-2-4成立, 而这两种情况下只需要把红色节点删除即可.其它情况并不符合红黑树的特性, 所以根本不会存在其它情况的删除.情况2-2-2: 待删除节点为黑色 & 待删除节点的右孩子为红色处理步骤:将其右孩子链接到其父节点上.将右孩子染为黑色即可.这种情况就是普通的节点删除操作示例图在下图红黑树中, 要删除节点25 按照上述的处理步骤进行调整, 调整之后的红黑树如下:
按照上述的处理步骤进行调整, 调整之后的红黑树如下: 直接把孩子节点染为黑色, 然后替换被删除节点的位置即可.情况2-2-2: 待删除节点为黑色 & 待删除节点的左孩子为红色处理步骤:将其左孩子链接到其父节点上.将左孩子染为黑色即可.这种情况就是普通的节点删除操作.示例图如同情况2-2-1的示例图, 只不过孩子节点在左边而已.情况3出现的情况情况3-1: 待删除节点为黑色情况3-1-1: 兄弟节点为红色情况3-1-2: 兄弟节点为黑色 & 兄弟节点的两个孩子有一个为红色情况3-1-3: 兄弟节点为黑色 & 兄弟节点的两个孩子都是黑色(包括NULL节点)情况3-2: 待删除节点为红色情况3-1-1: 待删除节点为黑色 & 兄弟节点为红色处理步骤(待删除节点是父节点的左孩子):父节点染为红色兄弟节点染为黑色对父节点进行左旋重新计算兄弟节点处理步骤(待删除节点是父节点的右孩子):父节点染为红色兄弟节点染为黑色对父节点进行右旋重新计算兄弟节点这时, 父节点为红色, 兄弟节点为黑色, 进入其它情况.示例图在下图红黑树中, 要删除节点5
直接把孩子节点染为黑色, 然后替换被删除节点的位置即可.情况2-2-2: 待删除节点为黑色 & 待删除节点的左孩子为红色处理步骤:将其左孩子链接到其父节点上.将左孩子染为黑色即可.这种情况就是普通的节点删除操作.示例图如同情况2-2-1的示例图, 只不过孩子节点在左边而已.情况3出现的情况情况3-1: 待删除节点为黑色情况3-1-1: 兄弟节点为红色情况3-1-2: 兄弟节点为黑色 & 兄弟节点的两个孩子有一个为红色情况3-1-3: 兄弟节点为黑色 & 兄弟节点的两个孩子都是黑色(包括NULL节点)情况3-2: 待删除节点为红色情况3-1-1: 待删除节点为黑色 & 兄弟节点为红色处理步骤(待删除节点是父节点的左孩子):父节点染为红色兄弟节点染为黑色对父节点进行左旋重新计算兄弟节点处理步骤(待删除节点是父节点的右孩子):父节点染为红色兄弟节点染为黑色对父节点进行右旋重新计算兄弟节点这时, 父节点为红色, 兄弟节点为黑色, 进入其它情况.示例图在下图红黑树中, 要删除节点5 按照上述的处理步骤进行调整, 调整之后的红黑树如下:
按照上述的处理步骤进行调整, 调整之后的红黑树如下: 这时还是不符合红黑树的性质, 需要进一步调整, 这时进入情况3-1-3.情况3-1-2: 待删除节点为黑色 & 兄弟节点为黑色 & 兄弟节点的两个孩子有一个为红色处理步骤(待删除节点是父节点的左孩子):判断兄弟节点的右节点是否是黑色(NULL节点为黑色)将兄弟节点的左孩子染为黑色将兄弟节点染为红色对兄弟节点进行右旋重新计算兄弟节点将兄弟节点的颜色染为父节点的颜色将父节点染为黑色将兄弟节点的右孩子染为黑色对父节点进行左旋处理步骤(待删除节点是父节点的右孩子):判断兄弟节点的左节点是否是黑色(NULL节点为黑色)将兄弟节点的右孩子染为黑色将兄弟节点染为红色对兄弟节点进行左旋重新计算兄弟节点将兄弟节点的颜色染为父节点的颜色将父节点染为黑色将兄弟节点的右孩子染为黑色对父节点进行右旋示例图以待删除节点是父节点的左孩子为例, 在下图红黑树中, 要删除节点15
这时还是不符合红黑树的性质, 需要进一步调整, 这时进入情况3-1-3.情况3-1-2: 待删除节点为黑色 & 兄弟节点为黑色 & 兄弟节点的两个孩子有一个为红色处理步骤(待删除节点是父节点的左孩子):判断兄弟节点的右节点是否是黑色(NULL节点为黑色)将兄弟节点的左孩子染为黑色将兄弟节点染为红色对兄弟节点进行右旋重新计算兄弟节点将兄弟节点的颜色染为父节点的颜色将父节点染为黑色将兄弟节点的右孩子染为黑色对父节点进行左旋处理步骤(待删除节点是父节点的右孩子):判断兄弟节点的左节点是否是黑色(NULL节点为黑色)将兄弟节点的右孩子染为黑色将兄弟节点染为红色对兄弟节点进行左旋重新计算兄弟节点将兄弟节点的颜色染为父节点的颜色将父节点染为黑色将兄弟节点的右孩子染为黑色对父节点进行右旋示例图以待删除节点是父节点的左孩子为例, 在下图红黑树中, 要删除节点15 按照上述的处理步骤进行调整, 调整之后的红黑树如下:
按照上述的处理步骤进行调整, 调整之后的红黑树如下: 调整完成.中间我们省略了步骤1中的处理步骤, 内部的处理步骤同插入时的调整类似, 把兄弟节点的红色孩子节点调整兄弟节点的右孩子(如果兄弟节点是左孩子的话, 那么就是将红色孩子节点调整为左孩子).其实这种情况下, 我们不关系待删除节点的父节点的颜色, 因为这种情况的调整是在内部进行调整的.情况3-1-3: 待删除节点为黑色 & 兄弟节点为黑色 & 兄弟节点的两个孩子都是黑色(包括NULL节点)注: 这里兄弟的孩子节点包括NULL节点.处理步骤:将兄弟节点染为红色将父节点染为黑色该情况与当待删除节点是父节点的左孩子还是右孩子无关, 因为不涉及旋转.当前节点指向父节点之后, 再看符合哪种调整情况, 继续进行调整.示例图情况3-1-1中调整之后树为:
调整完成.中间我们省略了步骤1中的处理步骤, 内部的处理步骤同插入时的调整类似, 把兄弟节点的红色孩子节点调整兄弟节点的右孩子(如果兄弟节点是左孩子的话, 那么就是将红色孩子节点调整为左孩子).其实这种情况下, 我们不关系待删除节点的父节点的颜色, 因为这种情况的调整是在内部进行调整的.情况3-1-3: 待删除节点为黑色 & 兄弟节点为黑色 & 兄弟节点的两个孩子都是黑色(包括NULL节点)注: 这里兄弟的孩子节点包括NULL节点.处理步骤:将兄弟节点染为红色将父节点染为黑色该情况与当待删除节点是父节点的左孩子还是右孩子无关, 因为不涉及旋转.当前节点指向父节点之后, 再看符合哪种调整情况, 继续进行调整.示例图情况3-1-1中调整之后树为: 按照上述的处理步骤进行调整, 调整之后的红黑树如下:
按照上述的处理步骤进行调整, 调整之后的红黑树如下: 调整完成.情况3-2: 待删除节点为红色这时, 父节点为黑色, 兄弟节点一定为红色. 因为此时待删除节点和兄弟节点都没有孩子节点.直接删除就好.删除总结删除时, 先看待删除节点的颜色, 然后查看其兄弟节点的颜色, 再查看兄弟节点的孩子节点的颜色, 然后根据具体的情况进行调整.参考TreeMap的删除调整代码/** From CLR */private void fixAfterDeletion(Entry<K,V> x) {
// 删除的节点为黑色时, 需要进行调整
while (x != root && colorOf(x) == BLACK) {
// 当前节点是左节点
if (x == leftOf(parentOf(x))) {
// 获取右节点(兄弟节点)
Entry<K,V> sib = rightOf(parentOf(x));
// 兄弟节点是红色时
if (colorOf(sib) == RED) {
// 兄弟节点染为黑色
setColor(sib, BLACK);
// 父节点染为红色
setColor(parentOf(x), RED);
// 对父节点进行左旋
rotateLeft(parentOf(x));
// 重新计算兄弟节点
sib = rightOf(parentOf(x));
}
if (colorOf(leftOf(sib)) == BLACK &&
colorOf(rightOf(sib)) == BLACK) { // 兄弟节点的两个孩子都是黑色
// 兄弟节点染为红色
setColor(sib, RED);
// 将当前节点指向父节点
x = parentOf(x);
} else { // 兄弟节点的两个孩子有一个为红色
// 判断兄弟节点红色孩子节点的位置
// 将兄弟节点的红色孩子节点调整到兄弟节点的右孩子节点位置
if (colorOf(rightOf(sib)) == BLACK) {
setColor(leftOf(sib), BLACK);
setColor(sib, RED);
rotateRight(sib);
sib = rightOf(parentOf(x));
}
// 将兄弟节点的颜色染为父节点的颜色
setColor(sib, colorOf(parentOf(x)));
// 父节点染为黑色
setColor(parentOf(x), BLACK);
// 兄弟节点的右孩子染为黑色
setColor(rightOf(sib), BLACK);
// 对父节点进行左旋
rotateLeft(parentOf(x));
// 退出循环
x = root;
}
} else { // symmetric
Entry<K,V> sib = leftOf(parentOf(x));
if (colorOf(sib) == RED) {
setColor(sib, BLACK);
setColor(parentOf(x), RED);
rotateRight(parentOf(x));
sib = leftOf(parentOf(x));
}
if (colorOf(rightOf(sib)) == BLACK &&
colorOf(leftOf(sib)) == BLACK) {
setColor(sib, RED);
x = parentOf(x);
} else {
if (colorOf(leftOf(sib)) == BLACK) {
setColor(rightOf(sib), BLACK);
setColor(sib, RED);
rotateLeft(sib);
sib = leftOf(parentOf(x));
}
setColor(sib, colorOf(parentOf(x)));
setColor(parentOf(x), BLACK);
setColor(leftOf(sib), BLACK);
rotateRight(parentOf(x));
x = root;
}
}
}
// 最后将当前节点染为黑色, 为什么需要这段代码? 我觉得你应该知道的.
setColor(x, BLACK);}
总结红黑树是一个比较重要的算法, 我觉得作为一个程序员应该需要了解它.红黑树的核心在于元素变动之后, 如何进行调整使其重新成为一颗红黑树.通过学习红黑树, 深刻体会到大问题并不可怕, 一点点拆分为小问题, 一定会解决的.文章不是一气呵成的, 个别地方可能会有问题, 如有发现, 烦请指出.JAVA算法作者:黑色毛衣Virgo链接:http://www.imooc.com/article/247142来源:慕课网本文原创发布于慕课网 ,转载请注明出处,谢谢合作推荐阅读:藏在正则表达式里的陷阱对于新手来说,Python 中有哪些难以理解的概念?Git使用教程,最详细,最傻瓜,最浅显,真正手把手教为什么部分程序员下班后只关显示器不关电脑?推荐10个Java方向最热门的开源项目为什么程序员应该有一台Mac个人电脑有哪些好笑的关于程序员的笑话?如何防止自己被人肉搜索到?如何写代码 —— 编程内功心法搞定JVM垃圾回收就是这么简单搞定计算机网络面试,看这篇就够了(补充版)
调整完成.情况3-2: 待删除节点为红色这时, 父节点为黑色, 兄弟节点一定为红色. 因为此时待删除节点和兄弟节点都没有孩子节点.直接删除就好.删除总结删除时, 先看待删除节点的颜色, 然后查看其兄弟节点的颜色, 再查看兄弟节点的孩子节点的颜色, 然后根据具体的情况进行调整.参考TreeMap的删除调整代码/** From CLR */private void fixAfterDeletion(Entry<K,V> x) {
// 删除的节点为黑色时, 需要进行调整
while (x != root && colorOf(x) == BLACK) {
// 当前节点是左节点
if (x == leftOf(parentOf(x))) {
// 获取右节点(兄弟节点)
Entry<K,V> sib = rightOf(parentOf(x));
// 兄弟节点是红色时
if (colorOf(sib) == RED) {
// 兄弟节点染为黑色
setColor(sib, BLACK);
// 父节点染为红色
setColor(parentOf(x), RED);
// 对父节点进行左旋
rotateLeft(parentOf(x));
// 重新计算兄弟节点
sib = rightOf(parentOf(x));
}
if (colorOf(leftOf(sib)) == BLACK &&
colorOf(rightOf(sib)) == BLACK) { // 兄弟节点的两个孩子都是黑色
// 兄弟节点染为红色
setColor(sib, RED);
// 将当前节点指向父节点
x = parentOf(x);
} else { // 兄弟节点的两个孩子有一个为红色
// 判断兄弟节点红色孩子节点的位置
// 将兄弟节点的红色孩子节点调整到兄弟节点的右孩子节点位置
if (colorOf(rightOf(sib)) == BLACK) {
setColor(leftOf(sib), BLACK);
setColor(sib, RED);
rotateRight(sib);
sib = rightOf(parentOf(x));
}
// 将兄弟节点的颜色染为父节点的颜色
setColor(sib, colorOf(parentOf(x)));
// 父节点染为黑色
setColor(parentOf(x), BLACK);
// 兄弟节点的右孩子染为黑色
setColor(rightOf(sib), BLACK);
// 对父节点进行左旋
rotateLeft(parentOf(x));
// 退出循环
x = root;
}
} else { // symmetric
Entry<K,V> sib = leftOf(parentOf(x));
if (colorOf(sib) == RED) {
setColor(sib, BLACK);
setColor(parentOf(x), RED);
rotateRight(parentOf(x));
sib = leftOf(parentOf(x));
}
if (colorOf(rightOf(sib)) == BLACK &&
colorOf(leftOf(sib)) == BLACK) {
setColor(sib, RED);
x = parentOf(x);
} else {
if (colorOf(leftOf(sib)) == BLACK) {
setColor(rightOf(sib), BLACK);
setColor(sib, RED);
rotateLeft(sib);
sib = leftOf(parentOf(x));
}
setColor(sib, colorOf(parentOf(x)));
setColor(parentOf(x), BLACK);
setColor(leftOf(sib), BLACK);
rotateRight(parentOf(x));
x = root;
}
}
}
// 最后将当前节点染为黑色, 为什么需要这段代码? 我觉得你应该知道的.
setColor(x, BLACK);}
总结红黑树是一个比较重要的算法, 我觉得作为一个程序员应该需要了解它.红黑树的核心在于元素变动之后, 如何进行调整使其重新成为一颗红黑树.通过学习红黑树, 深刻体会到大问题并不可怕, 一点点拆分为小问题, 一定会解决的.文章不是一气呵成的, 个别地方可能会有问题, 如有发现, 烦请指出.JAVA算法作者:黑色毛衣Virgo链接:http://www.imooc.com/article/247142来源:慕课网本文原创发布于慕课网 ,转载请注明出处,谢谢合作推荐阅读:藏在正则表达式里的陷阱对于新手来说,Python 中有哪些难以理解的概念?Git使用教程,最详细,最傻瓜,最浅显,真正手把手教为什么部分程序员下班后只关显示器不关电脑?推荐10个Java方向最热门的开源项目为什么程序员应该有一台Mac个人电脑有哪些好笑的关于程序员的笑话?如何防止自己被人肉搜索到?如何写代码 —— 编程内功心法搞定JVM垃圾回收就是这么简单搞定计算机网络面试,看这篇就够了(补充版)
实际上麻将游戏与其他的益智类的体育运动的最大的差别是有四个人一起玩的运动。与象棋围棋等不同,它们是两个人作战的,虽然桥牌也是四个人玩的,而实际是要分成两组来配合的。两组一起玩的互动再怎么复杂也还是有限制的,三方面的作战会限制的范围更大一些棋牌问答,麻将有四个人对战那就更为复杂了。从这一点来讲,反而麻将是虚幻的现实得更为实际的需要智商更加高层次的娱乐了。互联网使得虚拟相互变成了实际中,人们慢慢的由麻将桌上走出来棋牌问答,来到了虚拟的网络麻将游戏,可能是人们不喜欢面前实际的四人作战,太吵了,而想安静的享受属于自己的安静之地。或许是由于网络带给大家的想象的空间更多,网络中的游戏魅力的最大表现在,他是运用网络使得玩游戏的人们一起互相参与,这样互动使得在另一个世界的人们更多的参与进来。









