用 Breadth-first search 做 State space search，可获得从最少步骤至最多步骤的所有可行路径。以下代码设 a 为 M = 3 升杯的水，b 为 N = 4 升杯的水。#include <stdio.h> #define MIN(a, b) ((a) < (b) ? (a) : (b)) #define M 3 #define N 4 #define G 2 typedef struct State { int a, b; const struct State* parent; const char* action; }State; State q[(M + 1) * (N + 1)]; int front = 0, back = 0, visited[M + 1][N + 1]; void Enqueue(int a, int b, const State* parent, const char* action) { if (!visited[a][b]) { State t = { a, b, parent, action }; q[back++] = t; visited[a][b] = 1; } } void Backtrace(const State* s) { if (s) { Backtrace(s->parent); printf("(%d, %d) %s\n", s->a, s->b, s->action); } } int main() { Enqueue(0, 0, NULL, "Initialize"); while (front < back) { const State* s = &q[front++]; if (s->a == G || s->b == G) { Backtrace(s); printf("\n"); continue; } Enqueue(0, s->b, s, "Clear A"); Enqueue(s->a, 0, s, "Clear B"); Enqueue(M, s->b, s, "Fill A"); Enqueue(s->a, N, s, "Fill B"); int t1 = MIN(s->b, M - s->a); int t2 = MIN(s->a, N - s->b); Enqueue(s->a + t1, s->b - t1, s, "Fill A by B"); Enqueue(s->a - t2, s->b + t2, s, "Fill B by A"); } printf("Processed %d states\n", back); }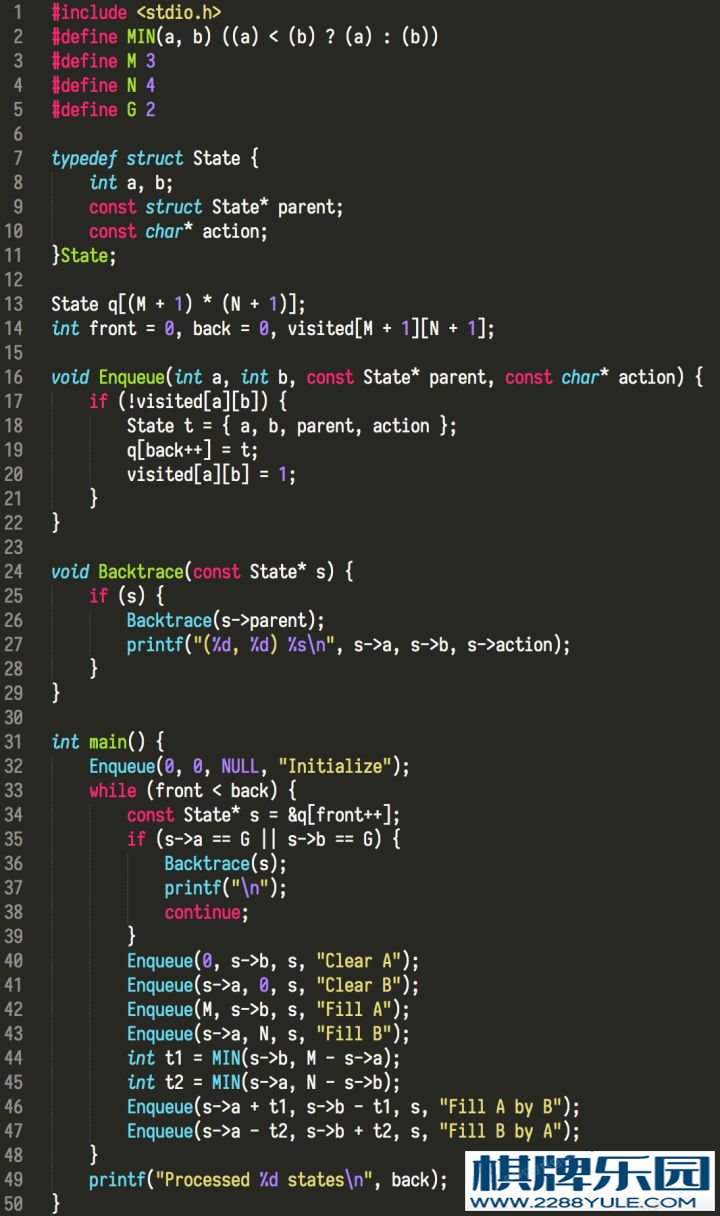编译输出：$ gcc -O3 water.c && time ./a.out (0, 0) Initialize (3, 0) Fill A (0, 3) Fill B by A (3, 3) Fill A (2, 4) Fill B by A (0, 0) Initialize (0, 4) Fill B (3, 1) Fill A by B (0, 1) Clear A (1, 0) Fill A by B (1, 4) Fill B (3, 2) Fill A by B Processed 12 states real 0m0.003s user 0m0.001s sys 0m0.001s2018/3/12 更新：写点解释。这个是典型的状态空间搜索问题。我们可以定义状态为 ， 是 升水杯（简称 A）的水量， 是 升水杯子（简称 B）的水量。初始状态为两杯皆空，即 。然后，合法的状态转移包括 6 种：把 A 全部清空（Clear A）；把 B 全部清空（Clear B）；把 A 倒满水（Fill A）；把 B 倒满水（Fill B）；把 A 的水倒至 B，最多令 B 全满（Fill B by A）；把 B 的水倒至 A，最多令 A 全满（Fill A by B）。目标状态为任一杯子的水量为 ，即 。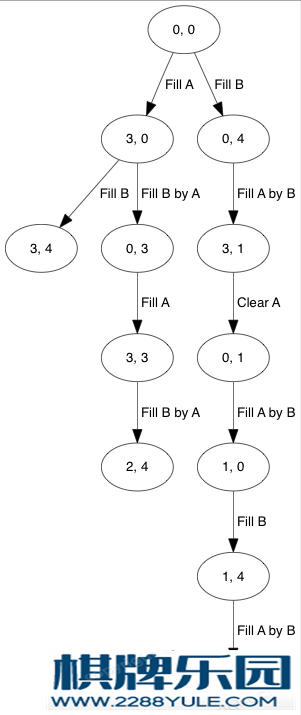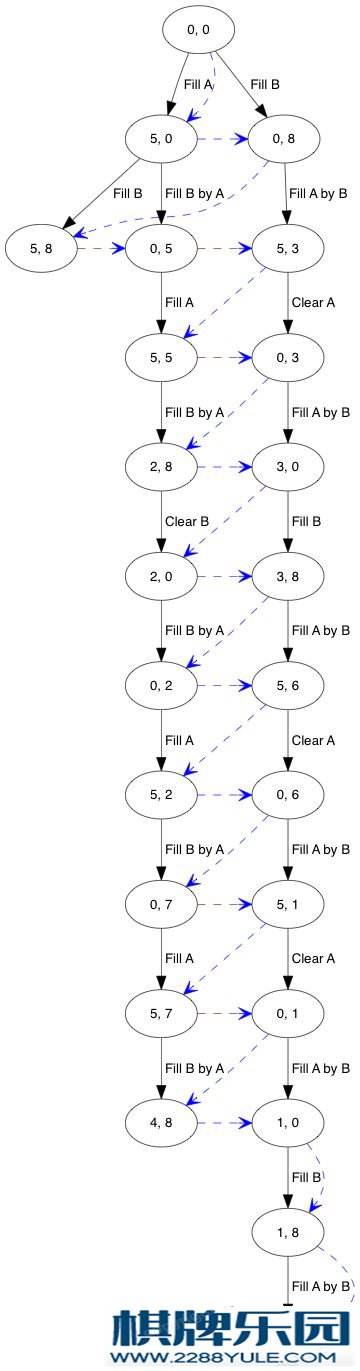根据上述的规则，我们可以生成以下的树，当中略去重复的状态转移：为了获取最优解，可使用 Breadth-first search 去遍历这个树，下图蓝箭头表示其遍历次序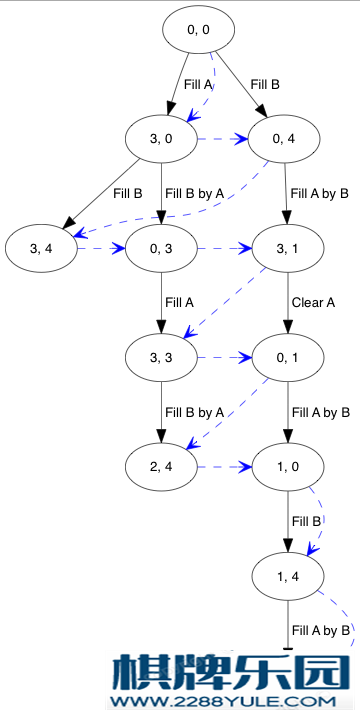：这算法需要一个队列去存储待展开的状态。在上面的代码，简单用了一个固定大小的数组q来实现（也可用动态数组或单链表）。最初我们加入初始状态：int main() { Enqueue(0, 0, NULL, "Initialize"); // ... }当队列非空，我们取出一个状态： while (front < back) { const State* s = &q[front++]; // ... }检查该状态是否达成目标，若然，则打印结果（如果只需最优结果，就不用 continue直接break便可）： if (s->a == G || s->b == G) { Backtrace(s); printf("\n"); continue; }否则，就尝试把状态转移： Enqueue(0, s->b, s, "Clear A"); Enqueue(s->a, 0, s, "Clear B"); Enqueue(M, s->b, s, "Fill A"); Enqueue(s->a, N, s, "Fill B"); int t1 = MIN(s->b, M - s->a); int t2 = MIN(s->a, N - s->b); Enqueue(s->a + t1, s->b - t1, s, "Fill A by B"); Enqueue(s->a - t2, s->b + t2, s, "Fill B by A");注意到，Enqueue() 里利用 visited[][]数组检查是否已遍历过相同的状态：int front = 0, back = 0, visited[M + 1][N + 1]; void Enqueue(int a, int b, const State* parent, const char* action) { if (!visited[a][b]) { State t = { a, b, parent, action }; q[back++] = t; visited[a][b] = 1; } }最后，我们找到目标状态，还要反向追踪这个状态来自哪个状态，直至到达最初状态。就是以下的红箭头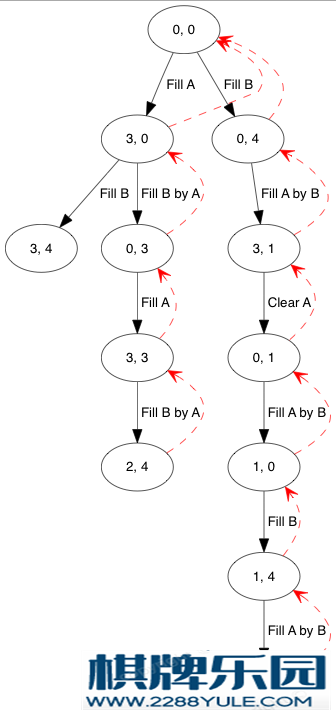：为此，我们在Enqueue()时，已保存状态的父状态及转移规则，以便反向追踪。如果我们按上面红色箭头把印的话，其打印次序是反过来的，因此这里用了递归的技巧去反转打印次序：static void Backtrace(const State* s) { if (s) { Backtrace(s->parent); printf("(%d, %d) %s\n", s->a, s->b, s->action); } }就是这样。最后，也许你会问，上面的图怎样画的？答案是修改程序，生成 DOT Language。2018/3/13：按 @打工战士 的评论更新代码。用宏表示杯子容量及目标，以 visited[][] 存储状态是否已被片历，并设置 q[]的大小。 这样可以处理任意容量和目标，例如 ：

后来，麻将机出现了，它的出现让麻将这个游戏变得很方便、很简洁棋牌百科，人们只需要轻松自在的玩游戏就行，不用再自己动手洗牌、台牌、摆牌，不用自己掷筛子，这些全都由它来自动完成，你只需要按动按钮就可以。打完之后也不用亲自动手费时费事的把麻将收起来，只需按动一个按钮，机器自动就把牌收起来、存储起来了，下次再玩只需按按钮棋牌百科，机子自动就把麻将洗好、整理好升至桌面上。也正是因为这些便捷性，使得人们更喜欢玩麻将一个有趣的游戏。